Šilumos kiekis, darbas, energija, faziniai virsmai
- Tarpdisciplininė užduotis. Savitoji žmogaus kūno šiluma yra \(3480\;\text{J/kg K}\) , tik šiek tiek žemesnė negu vandens. Šis skirtumas atsiranda dėl proteinų, riebalų ir mineralų, kurie sumažina specifinės šilumos reikšmę. Norint surasti šilumos kiekį, kuris pakeltų kūno temperatūrą nuo \(37^{\circ}\) iki \(44^{\circ}\) , naudosime šilumos kiekio apskaičiavimo formulę: \(Q=mc\Delta T=70\cdot3480\cdot7=1{,}7\cdot10^{6}\;\text{J}\) . \(1\; \text{W}=1\; \text{J/s}\) , tai \[ t=\frac{1{,}7\cdot10^{6}}{1200}=1400\; \text{s}=23\;\text{min} \]
- Šilumos kiekis, kurį vanduo atiduoda ataušdamas iki \(0\;^{\circ}\text{C}\) temperatūros: \(Q_{1}=c_{\text{vandens}}(m_{1}t_{1}+m_{2}t_{2})=16{,}8\;\text{kJ}\) . Lengva įsitikinti, kad šis šilumos kiekis yra mažesnis, negu reikalingas šilumos kiekis, kad išsilydytų visas ledas: \(Q=\lambda m_{3}=132\;\text{kJ}\) Tai reiškia, kad kalorimetre esančio vandens ir ledo temperatūra yra žemesnė arba lygi \(0\;^{\circ}\text{C}\) , \(\Theta\) \({\leq}\) \(0\;^{\circ}\text{C}\) . Iš kitos pusės, šylant ledui iki \(0\;^{\circ}\text{C}\) , išsiskirs šilumos kiekis: \(Q_{2}=c_{\text{ledo}}m_{3}t_{3}=50{,}4\;\text{kJ}\) . Toks šilumos kiekis yra per mažas, kad užšaltų visas vanduo, taigi kalorimetre esančio vandens ir ledo temperatūra yra aukštesnė arba lygi \(0\;^{\circ}\text{C}\) , \(\Theta{\geq}0\;^{\circ}\text{C}\) . Iš čia galima daryti išvadą, kad temperatūra kalorimetre yra lygi \(0\;^{\circ}\text{C}\) , \(\Theta = 0\;^{\circ}\text{C}\) .Vandens ataušimui ir ledo atšilimui iki šios temperatūros reikalingas šilumos kiekis yra \(Q=Q_{2}-Q_{1}=50{,}4-16{,}8=33{,}6\;\text{kJ}\) Šis šilumos kiekis gali išsiskirti tik užšąlant vandeniui, kurio masė \(\Delta m=\frac{Q}{\lambda}=0{,}1\;\text{kg}\) . Taigi, nusistovėjus termodinaminei pusiausvyrai, ledo masė padidės \(\Delta m=100\;\text{g}\) ir bus \(m=m_{3}+\Delta m=500\;\text{g}\) .
- Šilumos kiekis, atiduodamas sušildyti kūnui, yra proporcingas kūno ir jį supančios aplinkos temperatūrų skirtumui, todėl šilumos kiekis, išskiriamas radiatorių pirmuoju atveju iki atšalimo yra \(Q_{1}=k(t_{0}-t_{k_{1}})\) , kur \(k\) — radiatorių šilumos perdavimo koeficientas.Esant pusiausvyrai, toks pats šilumos kiekis išskiriamas lauke: \(Q_{2}=k(t_{0}-t_{k_{1}})=K(t_{k_{1}}-t_{1})\) , kur \(K\) — pastato šilumos perdavimo koeficientas.Iš šių dviejų lygčių randame, kad \(t_{k_{2}}=\frac{t_{0}+\left(K/k\right)t_{2}}{1+\left(K/k\right)}\) , kur \(\frac{K}{k}=\frac{t_{0}-t_{k_{1}}}{t_{k_{1}}-t_{1}}\) Įrašius skaitines vertes, gauname, kad \(K / k {\approx} 0{,}86\); \(t_{k_{2}}\approx15{,}8\;{^\circ}\text{C}\) . Taigi, atėjus šalčiams būtina padidinti radiatorių temperatūrą. Pagal Lietuvos higienos normą HN 42:2004, komfortabili kambarių temperatūra šaltuoju metų laiku yra \(19 – 23\;{^{\circ}\text{C}}\) .
- Reikalingas šilumos kiekis ledą paversti į garus yra \(Q=Q_{1}+Q_{2}+Q_{3}+Q_{4}\) ,kur \(Q_1\) — šilumos kiekis, išskiriamas ledui šylant iki jo lydymosi temperatūros, t.y. \(t_{\text{lyd}}=0^{\circ}\text{C}\) \[ Q_{1}=c_{1}m(t_{\text{lyd}}-t_{1}) \] \(Q_2\) — šilumos kiekis, išskiriamas ledui virstant vandeniu, t.y. ledo lydymosi šilumos kiekis \[ Q_{2}=\lambda m \] \(Q_3\) — šilumos kiekis, išskiriamas vandeniui šylant iki \(t_2\) \[ Q_{3}=c_{2}m(t_{2}-t_{\text{lyd}}) \] \(Q_4\) — šilumos kiekis, išskiriamas vandeniui virstant garais, t.y. vandens garavimo šilumos kiekis \[ Q_{4}=Lm \] Įstačius šias išraiškas į pirmąją šilumos kiekio skaičiavimo formulę, gauname \(Q=m\left(c_{1}(t_{\text{lyd}}-t_{1})+\lambda+c_{2}(t_{2}-t_{\text{lyd}})+L\right)=60{,}81\;\text{kJ}\).
- Šilumos kiekis, išsiskiriantis šylant ledui iki \(0\;^{\circ}\text{C}\) temperatūros: \(Q_{2}=c_{2}m_{2}(t_{\text{lyd}}-t_{2})=16{,}8\;\text{kJ}\).Šilumos kiekis, kurį vanduo atiduoda ataušdamas iki \(0\;^{\circ}\text{C}\) temperatūros: \(Q_{1}=c_{1}m_{1}(t_{1}-t_{\text{lyd}})=12{,}57\;\text{kJ}\).Matome, kad norint viso ledo temperatūrą pakelti iki \(0\;^{\circ}\text{C}\) temperatūros trūksta \(Q=Q_{2}-Q_{1}=42{,}30\;\text{kJ}\). Toks šilumos kiekis išsiskirs tam tikros masės m3 vandeniui virstant į ledą \[ Q_{2}-Q_{1}=\lambda m_{3} \] iš kur \(m_{3}=\frac{Q_{2}-Q_{1}}{\lambda}=12{,}8\;\text{g}\) Taigi galutiniu atveju, esant temperatūrai \(\Theta=0\;^{\circ}\text{C}\) inde bus \(m_{2}+m_{3}=412{,}8\;\text{g}\) ledo ir \(m_{1}-m_{3}=287{,}2\;\text{g}\) vandens.
- Geležies tankis \(\rho=\frac{m}{V}\) įdėjimo į indą metu yra susijęs su jos tankiu, esant \(0\;^{\circ}\text{C}\) temperatūrai ir yra lygus \(\rho=\frac{\rho_{0}}{1+\beta t}\) . Iš čia, žinant tankių \(\rho\) ir \(\rho_0\) reikšmes, galima nustatyti geležies temperatūrą: \[ t=\frac{\rho_{0}-\rho}{\beta\rho}=\frac{V\rho_{0}-m}{\beta m} \] Ledo masė, nusistovėjus pusiausvyrai, galima apskaičiuoti pagal \[ m_{\text{ledo}}=\frac{mc}{\lambda}t=\frac{mc}{\lambda}\frac{V\rho_{0}-m}{\beta m} \] \(m_{\text{ledo}}\approx64\) g.
- Iš pirmosios grafiko dalies matome, kad per \(\Delta t_{1}=60\; \text{s}\) vyksta ledo ir kietos būsenos nežinomos medžiagos šilimo procesas nuo \(t_{1}=-40^{\circ}\text{C}\) iki \(t_{2}=-20\;^{\circ}\text{C}\) . Pažymėjus šildytuvo galią N, galima parašyti šio proceso šiluminio balanso lygtį: \(m\left(c_{\text{ledo}}+c\right)\left(t_{2}-t_{1}\right)=N\Delta t_{1}\) , kur \(m = 1\;\text{kg}\) ledo (ji lygi nežinomos medžiagos masei). Antruoju laiko momentu, \(\Delta t_{2}=100\; \text{s}\) vyksta medžiagos lydymasis, kai temperatūra yra \(t_{2}=-20\;^{\circ}\text{C}\) , todėl \[ \lambda m=N\Delta t_{2} \] Galiausiai, trečiuoju laiko momentu, \(\Delta t_{3}=80\; \text{s}\) vyksta ledo ir išsilydžiusios medžiagos šilimas nuo \(t_{2}=-20\;^{\circ}\text{C}\) iki \(t_{3}=0\;^{\circ}\text{C}\) .Šio proceso šilumos balanso lygtis yra \(m\left(c_{\text{ledo}}+c_{1}\right)\left(t_{3}-t_{2}\right)=N\Delta t_{3}\) Iš gautų lygčių randame \(\lambda=\left(c_{\text{ledo}}+c\right)\left(t_{2}-t_{1}\right)\frac{\Delta t_{2}}{\Delta t_{1}}=10^{5}\) J/kg \(c_{1}=\left(c_{\text{ledo}}+c\right)\frac{t_{2}-t_{1}}{t_{3}-t_{2}}\cdot\frac{\Delta t_{3}}{\Delta t_{1}}-c_{\text{ledo}}=2\cdot10^{3}\;\text{J/kg} {^{\circ}}\text{C}\))
- Reikalingas šilumos kiekis ledui virsti vandeniu \(Q=\lambda m_{\text{ledo}}\) išsiskiria kondensacijos metu tam tikros masės \(m_{\text{garų}}\) garų pavidalu ir atsiradusio vandens aušimo metu iki \(0\;^{\circ}\text{C}\) temperatūros. Taigi, šiluminio balanso lygtis, šiuo atveju, gali būti užrašoma: \(\lambda m_{\text{ledo}}-Lm_{\text{garų}}+m_{\text{garų}}c(t_{\text{ledo}}-t_{\text{garų}})=0\) ,Kur L — savitoji garavimo šiluma, c — savitoji vandens šiluma.Iš čia galima išsireikšti garų masę: \[ m_{\text{garų}}=m_{\text{ledo}}\frac{\lambda}{L+c(t_{\text{garų}}-t_{\text{ledo}})} \] Pilna atsiradusio vandens masė yra \(m=m_{\text{ledo}}+m_{\text{garų}}=m_{\text{ledo}}\left(1+\frac{\lambda}{L+c(t_{\text{garų}}-t_{\text{ledo}})}\right)=112\;\text{g}\).
- Suprantama, kad viso proceso aprašymas vyks dvejais etapais: visų pirma, vanduo atšals nuo \(20\;^{\circ}\text{C}\) iki \(0\;^{\circ}\text{C}\) temperatūros ( \(\Delta t=20\;^{\circ}\text{C}\) ), o po to, pusė vandens pavirs ledu, esant pastoviai \(0\;^{\circ}\text{C}\) temperatūrai. Tokiu atveju, pirmajame etape vanduo atiduos šilumos kiekį \(Q_{1}=cm_{1}\Delta t\) , o antrajame etape — \(Q_{2}=\frac{\lambda m_{1}}{2}\) . Atiduota vandens šiluma bus naudojama azoto garavimui. Taigi, m pažymėjus išgaravusį azotą, šilumos balanso lygtį galima užrašyti taip: \[ Q_{1}+Q_{2}=cm_{1}\Delta t+\frac{\lambda m_{1}}{2}=Lm \] Iš čia, ieškoma azoto masė: \(m=\frac{\left(c\Delta t+\frac{\lambda}{2}\right)m_{1}}{L}=1{,}27\;\text{kg}\)
- Kristalizacijos procesas baigsis tuomet, kai vanduo ir susidaręs ledas bus \(0\;^{\circ}\text{C}\) temperatūros. Vandens masę pažymime \(m_1\), o susidariusio ledo masę — \(m_2\). Rasime vandens vidinės energijos pokytį susidarant ledui:vanduo \(m_1- m_2\) masės liko skystoje būsenoje ir sušilo nuo \(-10\) iki \(0\;^{\circ}\text{C}\) . Reiškia, kad jo vidinė energija padidėjo \(10(m_1 — m_2)\;\text{cal}\) ; vanduo \(m_2\) masės pavirto ledu. Norint išskaičiuoti jo vidinės energijos pokytį, laikysime, kad vanduo iš pradžių sušilo nuo \(-10\) iki \(0\;^{\circ}\text{C}\) , o paskui sukietėjo. Iš to seka, kad jo vidinė energija pakito \(10m_2 — 80m_2\;\text{cal}\), t.y. sumažėjo \(70m_2\;\text{cal}\).Tokiu atveju, \[ \Delta U=10(m_{1}-m_{2})-70m_{2} \] Kadangi šilumos perdavimas vyksta tik tarp vandens ir ledo, tai \[ 10(m_{1}-m_{2})-70m_{2}=0 \] Iš čia \[ \frac{m_{1}}{m_{2}}=0{,}125=12{,}5\% \]
- Vagono kinetinė energija: \(E_{k}=\frac{mv^{2}}{2}=\frac{20000\cdot20^{2}}{2}=4\cdot10^{6}\;\text{J}\) Oro masė vagone: \(m=\rho V=1{,}3\cdot120=156\;\text{kg}\) Temperatūros pokytis: \(\Delta t=\frac{E_{k}}{mc}=\frac{4\cdot10^{6}}{156\cdot1000}\approx26\;^\circ\text{C}\).
- Atmosferinis oras atliko darbą: \(A=p_{0}S\delta\) ,kur \(p_0\) — atmosferinis slėgis, \(S\) — inde esančio gyvsidabrio paviršiaus plotas ir \(\delta\) — inde esančio gyvsidabrio sumažejimas, atsukus kraną.Kadangi \(p_{0}=\rho gh\) ir \(S\delta=sh\) , kur \(\rho\) — gyvsidabrio tankis, o \(s\) — vidinis vamzdelio skerspjūvio plotas, tai darbą galima apskaičiuoti \(A=\rho ghsh=mgh\) , kur \(m=\rho hs\) — sumažėjusio gyvsidabrio masė. Skaičiuodami, kad potencinė gyvsidabrio energija padidėjo \[ \Delta W_{p}=\frac{mgh}{2} \] prieiname išvados, kad ieškomas šilumos kiekis yra \[ Q=A-\Delta W_{p}=\frac{mgh}{2} \]
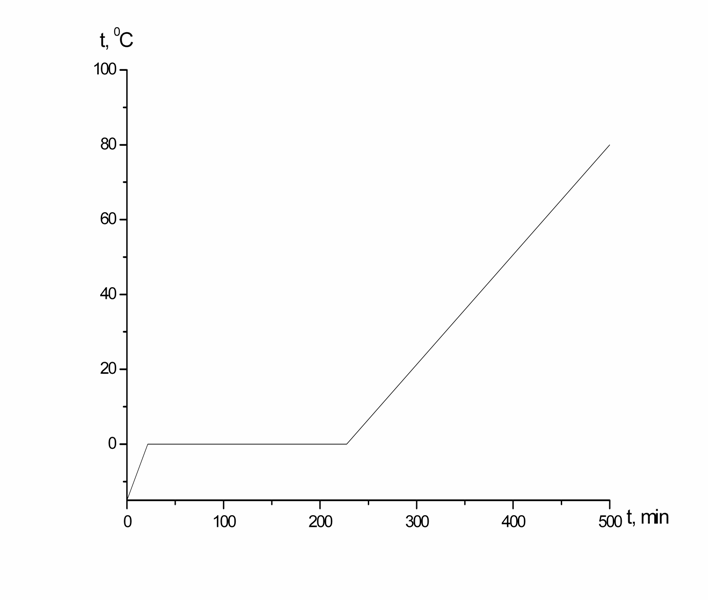
- šilumos kiekis, reikalingas norint pakelti ledo temperatūrą iki \(0\;^{\circ}\text{C}\) : \(Q=mc\Delta t=0{,}55\cdot2{,}1\cdot10^{3}\cdot15=1{,}73\cdot10^{4}\;\text{J}\) Laikas, per kurį įvyks šis procesas: \(t=\frac{1{,}73\cdot10^{4}}{800}=21{,}6\;\text{min}\)
- šilumos kiekis, reikalingas norint ištirpdinti visą ledą: \(Q=m\lambda=0{,}55\cdot3{,}3\cdot10^{5}=1{,}82\cdot10^{5}\;\text{J}\) Laikas, per kurį įvyks šis procesas: \(t=\frac{1{,}82\cdot10^{5}}{800}=227{,}5\;\text{min}\) Nuo kaitinimo pradžios iki visiško ledo ištirpimo praeis \(249{,}1\;\text{min}\)
- Žymiai daugiau laiko užtrunka ledui išsilydyti negu pasiekti lydymosi temperatūrą:
- Šilumos kiekis, reikalingas norint pakelti ledo temperatūrą iki \(0\;^{\circ}\text{C}\) , \(t_{0}=0\;^{\circ}\text{C}\) : \(Q_{1}=c_{1}m_{1}(t_{0}-t_{1})=44{,}5\cdot10^{3}\;\text{J}\). Šilumos kiekis, reikalingas norint atvėsinti vandens temperatūrą iki \(0\;^{\circ}\text{C}\) : \(Q_{2}=c_{2}m_{2}(t_{2}-t_{0})=6{,}3\cdot10^{3}\;\text{J}\) . \(Q_{3}=\lambda m_{2}=33{,}4\cdot10^{3}\;\text{J}\) Matome, kad \(Q_1> Q_2 + Q_3\), todėl galutinė temperatūra kalorimetre bus neigiama, vanduo atvės iki \(0\;^{\circ}\text{C}\) , užšals ir šis užšalęs ledas bus temperatūros \(t_3\).Galutinė šilumos balanso lygtis: \[ c_{1}m_{1}(t_{3}-t_{1})=c_{2}m_{2}(t_{2}-t_{0})+\lambda m_{2}+c_{1}m_{2}(t_{0}-t_{3}) \] arba \[ t_{3}\left(1+\frac{m_{2}}{m_{1}}\right)=t_{1}+\frac{c_{2}m_{2}}{c_{1}m_{1}}t_{2}+\frac{\lambda m_{2}}{c_{1}m_{1}} \] iš čia gauname, kad \(t_{3}=-4{,}6\;^{\circ}\text{C}\)

